3種類の品物の合計代金（不定方程式）

問題

　太郎君と花子さんは、学校の花壇に植えるチューリップの球根を買いに行きます。

太　郎：球根を全部で50個買えばいいんだよね。予算は6500円だから、1個130円の球根を買えばいいんだよね。

花　子：待って、130円の球根はないわ。色や花の大きさによって、150円、120円、90円の3種類の値段があるみたい。

太　郎：そうしたら、一番安い90円の球根を50個買っておつりを持って帰ればいいんじゃないかな。

花　子：せっかくだから、おつりができるだけ少なくなるようにしましょうよ。それに1種類だけにするんじゃなくて、3種類それぞれをできるだけ多く、どれも10個以上買いましょうよ。

太　郎：それがいいね。そうしたら、それぞれを何個買えばいいのか考えよう。ちょっと複雑だから、表にして考えようか。

花　子：とりあえず、120円の球根を50個買えば6000円よね。そこから考えてみましょう。

太　郎：おつりができるだけ少なくなるには、ここから120円の球根を150円の球根に交換してみればいいんじゃないかな。（表1）

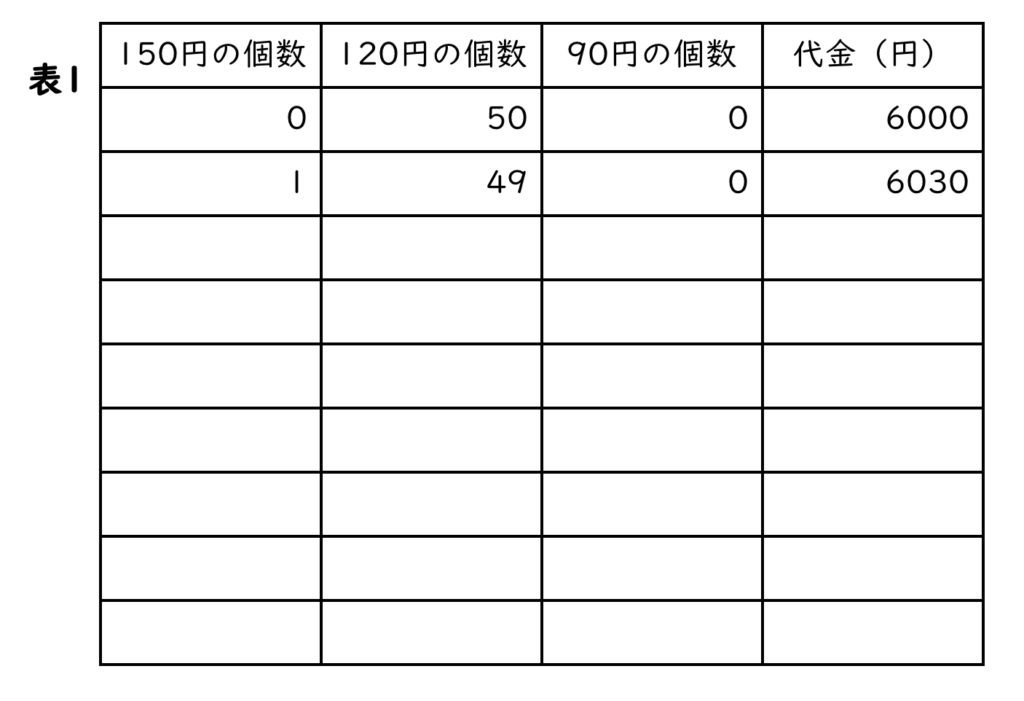
〔問題1〕2人の会話と表1を参考に、3種類の球根を何個ずつ買えばよいか求めなさい。

出題のポイント

3種類の品物の個数と代金、いわゆるつるかめトンボ算、不定方程式の問題です。私立併願組にとってもそれなりの難問ですが、表の誘導があるのでそれを軸に攻めていきましょう。解き方を知っているならば先に30個買う、という方法からスタートする方が圧倒的に簡単です。

PDFファイル

プリントのダウンロード

3種類の品物の合計代金

1 file(s) 75 KB

Download