地図と地球儀の違い
問題
花子さんと太郎君は、校外学習のまとめとして、1964(昭和39)年から2016(平成28)年までの間にオリンピック・パラリンピックが開かれた都市について調べてみました。
花 子:オリンピック・パラリンピックが開かれた都市は、世界各地に散らばっているわね。
太 郎:東京から遠い都市が多いね。そういえば、僕の好きな種目を見たくても、夜中に放送されたので、見られなくて残念だったことを覚えているよ。
花 子:東京から、オリンピック・パラリンピックが開かれた都市まで、どのくらいの距離があるのか測ってみましょう。社会の教科書に、地球儀を使って測る方法が出ていたわ。
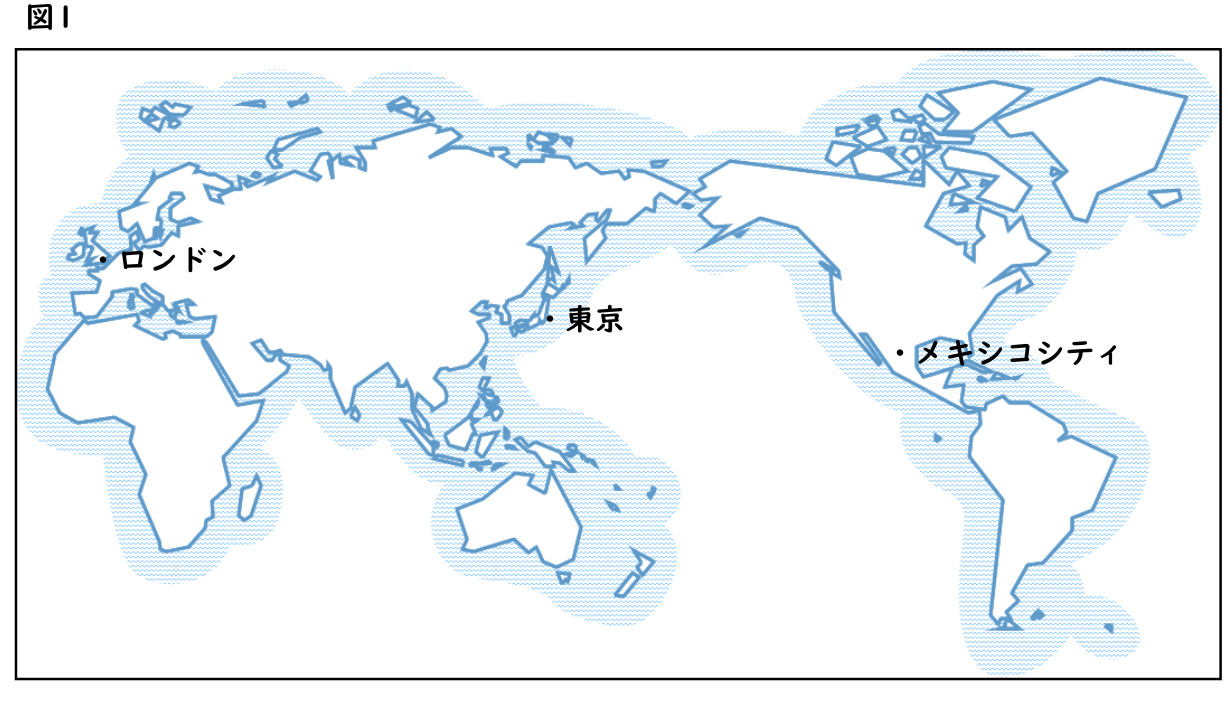
太 郎:地球儀でなく、この地図(図1)を使って測ってもいんじゃないかな。
先 生:この地図で距離を測ろうとすると、正確に測ることができないんだよ。
花 子:それはどうしてなのですか。
先 生:では、ロンドンとメキシコシティの2つの都市を取り上げ、この地図と地球儀を使い、東京との距離を測ってみましょう。
【地図を使った手順(8500万分の1の地図を使用】
①地図上にある2つの都市と東京との間の長さを測る
②その長さを8500万倍しておよその距離を出す
【地球儀を使った手順(5000万分の1の地球儀を使用】
①地球儀上にある2つの都市と東京との間に紙テープを貼る
②平らな場所で、その紙テープの長さを測る
③その長さを5000万倍しておよその距離を出す
花子さんと太郎君がこの地図と地球儀で調べた結果、表1のようになりました。

花 子:確かに、この地図で測ると、実際の距離と大きく違うところが出てきてしまうわね。
太 郎:どうしてなのだろう。
〔問題1〕 表1でわかるように、地球上の2つの都市の間の距離を測るばあい、地図を使った手順では、地球儀を使った手順よりも、実際の距離と大きく違っていました。 地図のほうが地球儀よりも実際の距離との違いが大きくなるのはなぜなのか、地図と地球儀との違いを挙げながら説明しなさい。
出題のポイント
地球儀と地図で、縮尺を使って実際の距離を計算した場合に、地図のほうが誤差が大きくなった理由を説明する問題です。
地理、もしくは地学の知識として、図5の地図がメルカトル図法で、高緯度地方(南北の端)を引き延ばすことで球形の地球を長方形の地図に写していることを知っていれば簡単です。
そこまでの知識がなくとも、長方形の地図をどう丸めても球にできないことを考えれば、球を長方形の地図にする際に、どこかで縮小率がずれることがわかるはずです。
PDFファイル
地図と地球儀の違いプリントのダウンロード
-
前の記事

一問一答 音の性質 2020.03.16
-
次の記事

一問一答 季節と生物 2020.03.16