てこの性質
問題
太郎君と花子さんは、実験用てこ(以下「てこ」といいます)を使い、おもりのつり下げかたと、てこが水平につり合うことについて考えてみました。 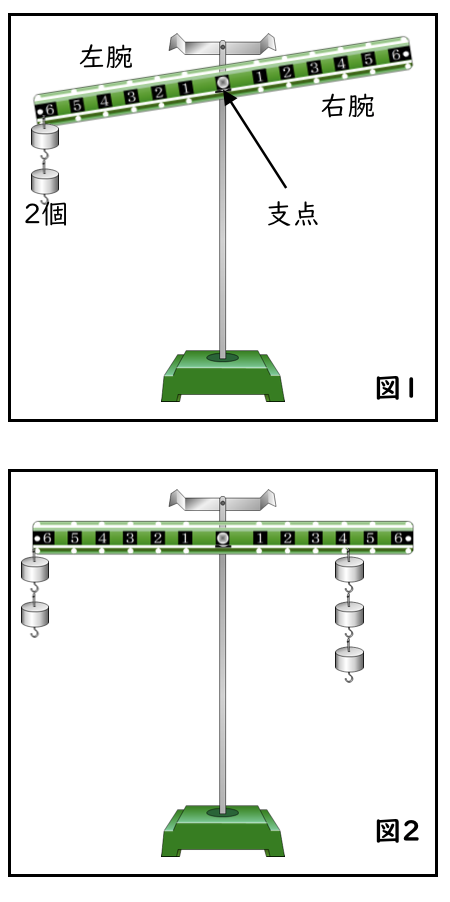
右の図1のように、てこには、中央を支点とした棒の左右の腕に、支点から同じ間隔でおもりをつり下げる穴 があいています。穴には、支点〜近い順に1⃣〜6⃣の番号がついていて、おもりの位置を表しています。図1のように、てこの左の6⃣に1個15gのおもりが2個つり下がっていて、左の腕が下がっています。
そこで、てこが水平につり合う条件について確かめてみました。
太 郎:右の4⃣に、1個15gのおもりを3個つり下げるとつり合うね。これはどうしてだろう。
花 子:てこを回すはたらきが左右で等しくなったからだわ。回すはたらきが右の腕が(15×2)×6=180、左の腕が(15×3)×4=180になっているもの。
太 郎:てこを回すはたらきを計算で求められるんだね。右の腕のおもりの位置やつり下げるおもりの個数を変えて、いろいろ確かめてみようよ。
〔問題1〕右の腕の1か所に、1個15gのおもりをいくつつり下げても、てこが水平につり合わないおもりの位置があることが分かりました。そのおもりの位置はどこか答えなさい。また、そのように考えた理由を、式と言葉で説明しなさい。
太 郎:おもりをつり下げる所を1か所じゃなく、2か所以上につり下げてみようよ。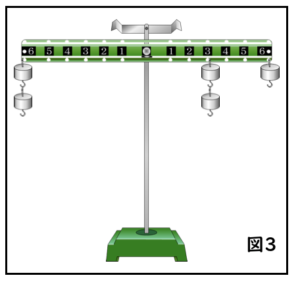
花 子:1個15gのおもりを右の3⃣に2個、6⃣に1個つり下げると、てこが水平につりあったわ(図3)。
太 郎:てこを回すはたらきが、右の腕は(15×1)×6+(15×2)×3=180になっているね。
花 子:腕の2か所以上におもりをつり下げたときは、それぞれの(おもりの重さ)×(おもりの位置)をたせばいいのね。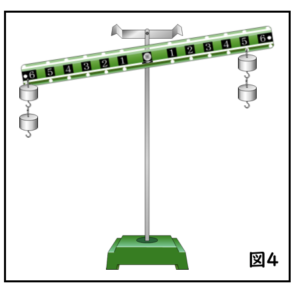
太 郎:じゃあ、右の5⃣に、1個15gのおもりを2個つり下げてみて、あと1か所おもりをつり下げてつり合わせてみようよ(図4)。
〔問題2〕右の腕の5⃣以外のもう1か所に、1個15gのおもりをつり下げててこを水平につり合わせるためには、右の腕のどの位置に何個つり下げればよいか説明した、次の文の【 あ 】【 い 】にあてはまる数字の組み合わせをすべて答えなさい。なお、解答欄はすべて使うとは限りません。
「おもりの位置が【 あ 】のところに【 い 】個つり下げる。」
花 子:重さの異なるおもりも使ってみましょう。ここに30gのおもりが1個あるわ。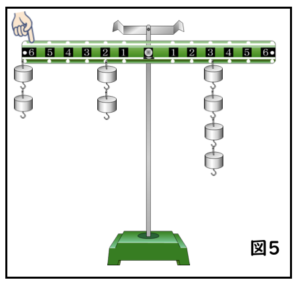
太 郎:じゃあ、まずは1個15gのおもりを左の6⃣に2個、2⃣に2個、右の3⃣に4個つり下げてみよう。これだとてこが回っちゃうから、指で止めておくね。
花 子:残っているおもりは15gが1個と、30gが1個ね。これを使ってつり合わせてみましょう。
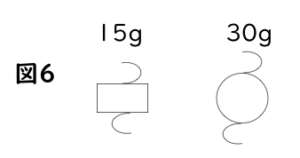
〔問題3〕図5のてこが、指を離しても水平につり合うように、右の腕に15gのおもり1個、左の腕に30gのおもり1個を、解答欄の図に書きなさい。ただし、おもりの形は下の図6をもとにし、すでにつり下がっているおもりの下にはつり下げないものとします。
出題のポイント
大問形式のてこ計算問題です。
モーメント計算のルールは説明してくれていますが、この程度のルールは受検生ならば覚えているでしょう。
私立併願者にとってはかなり簡単な問題になります。
(3)は条件を読み落とさないよう注意してください。

